Kapitel 14 Regression
Regression ist ein riesiges Thema, und der Umstand, dass ich ein 600-seitiges Buch dazu habe, sollte euch ein grobes Gefühl dafür geben, wie umfangreich es sein kann.
In QM1 schauen wir uns die Regression nur in einem relativ simplen Kontext an: Lineare Regression.
Weiterhin interessieren wir uns (vorerst) noch nicht für p-Werte, t-Statistiken und Signifikanz, und auch Modellgütekriterien sind erstmal uninteressant.
Wir benutzen Regression hier erstmal ausschließlich zur Evaluation linearer Zusammenhänge.
Also los.
14.1 Einfache Lineare Regression
Mal angenommen, wir wollen wissen ob bei Game of Thrones im Laufe der Serie mehr gestorben wird, sprich wir wollen wissen, ob es einen positiven Zusammenhang zwischen der Staffel und der Anzahl der Tode pro Staffel gibt. Dafür müssen wir unseren gotdeaths-Datensatz etwas umtransformieren:
library(dplyr)
gotdeaths_perseason <- gotdeaths %>%
group_by(death_season) %>%
summarize(deaths = n())
knitr::kable(gotdeaths_perseason)| death_season | deaths |
|---|---|
| 1 | 11 |
| 2 | 10 |
| 3 | 9 |
| 4 | 17 |
| 5 | 13 |
| 6 | 40 |
Jetzt haben wir zwei simple Variablen: Die Staffel und die Anzahl der Tode pro Staffel. Damit lässt sich arbeiten. Vorher wollen wir uns das aber erstmal kurz anschauen:
library(ggplot2)
ggplot(data = gotdeaths_perseason, aes(x = death_season, y = deaths)) +
geom_point(size = 3) +
geom_smooth(method = lm, se = FALSE, color = "red") +
scale_x_continuous(breaks = 1:6) +
labs(title = "Game of Thrones", subtitle = "Deaths per Season",
x = "Season", y = "Deaths")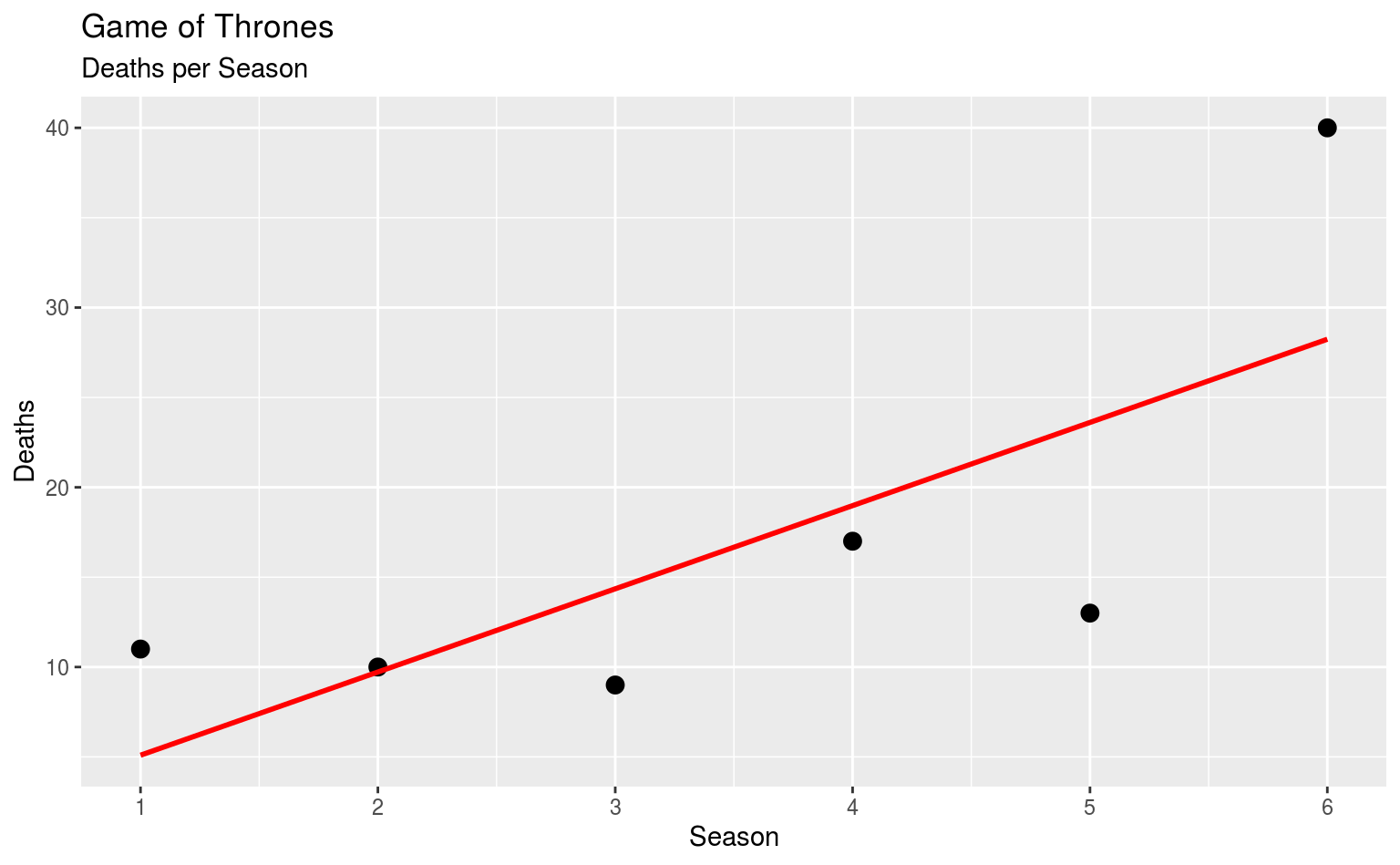
In diesem einfachen Scatterplot haben wir auch gleich eine Regressionsgerade via geom_smooth(method = lm),
das ist die gleiche Gerade, die durch unsere Regressionkoeffizienten definiert wird.
Und wo kommen die her?
Aus lm – der Funktion, mit der wir lineare Modelle erstellen.
14.1.1 Modelle erstellen
14.1.2 Das Modell-Objekt
In den meisten Quellen zum Thema werdet ihr vermutlich jetzt darauf gestoßen, das Output von lm in summary zu stecken, was zwar die relevanten Ergebnisse liefert, dabei aber leider unschön aussieht:
#>
#> Call:
#> lm(formula = deaths ~ death_season, data = gotdeaths_perseason)
#>
#> Residuals:
#> 1 2 3 4 5 6
#> 5.9048 0.2762 -5.3524 -1.9810 -10.6095 11.7619
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.4667 8.3061 0.056 0.9579
#> death_season 4.6286 2.1328 2.170 0.0958 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 8.922 on 4 degrees of freedom
#> Multiple R-squared: 0.5407, Adjusted R-squared: 0.4259
#> F-statistic: 4.71 on 1 and 4 DF, p-value: 0.09579Eine kompaktere Variante finden wie im package broom:
| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | 0.467 | 8.306 | 0.056 | 0.958 |
| death_season | 4.629 | 2.133 | 2.170 | 0.096 |
Hier ist tidy dazu da, die Koeffizienten als einfachen data.frame auszuspucken, das sich besser zur Darstellung in einer Tabelle eignet. Hier fehlt uns jetzt aber beispielsweise das \(R^2\), aber natürlich gibt’s auch da was:
| deaths | |||
|---|---|---|---|
| Predictors | Estimates | CI | p |
| (Intercept) | 0.47 | -15.81 – 16.75 | 0.958 |
| death_season | 4.63 | 0.45 – 8.81 | 0.096 |
| Observations | 6 | ||
| R2 / R2 adjusted | 0.541 / 0.426 | ||
Generell würde ich das Package sjPlot bzw. die Funktion tab_model zur Darstellung von Regressionsmodellen empfehlen: Die Funktion ist von Haus aus auf hübsches Output ausgelegt, und ist ausreichend modifizierbar um das Output so spartanisch oder umfassend wie gewünscht aussehen zu lassen.
Wenn ihr mit den Innereien eines Regressionsmodells rumspielen möchtet, gibt’s da auch was in broom:
| deaths | death_season | .fitted | .se.fit | .resid | .hat | .sigma | .cooksd | .std.resid |
|---|---|---|---|---|---|---|---|---|
| 11 | 1 | 5.095 | 6.457 | 5.905 | 0.524 | 9.041 | 0.506 | 0.959 |
| 10 | 2 | 9.724 | 4.848 | 0.276 | 0.295 | 10.301 | 0.000 | 0.037 |
| 9 | 3 | 14.352 | 3.795 | -5.352 | 0.181 | 9.720 | 0.049 | -0.663 |
| 17 | 4 | 18.981 | 3.795 | -1.981 | 0.181 | 10.225 | 0.007 | -0.245 |
| 13 | 5 | 23.610 | 4.848 | -10.610 | 0.295 | 7.273 | 0.420 | -1.416 |
| 40 | 6 | 28.238 | 6.457 | 11.762 | 0.524 | 3.050 | 2.007 | 1.910 |
Hier haben wir für jeden der Ausgangswerte noch den prognostizierten Wert .fitted, das Residuum .resid und diverse andere Statistiken, die uns vorerst nicht weiter interessieren.